Topic 1-2: One, two and three-dimensional spaces
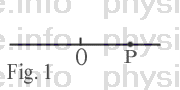 Let us consider a line, take a point on the line, and call it the origin, denoted as
O as in Fig. 1. We can determine a distance to any point P from the origin O, using the concept of
distance and the measurement system of length as discussed in Topic 1-1. Thus, any point
on the line can be represented by a real number, its distance from the origin O. The
assembly of all the points, each of which can be represented by a real number, is called
a one-dimensional space. Thus, the line under consideration is a one-dimensional space.
However, a one-dimensional space is more general than a straight line. A
curved line, open or closed, is also a one-dimensional space since each point on it can
also be represented by a real number, the distance from the origin that can be picked
artificially.
Let us consider a line, take a point on the line, and call it the origin, denoted as
O as in Fig. 1. We can determine a distance to any point P from the origin O, using the concept of
distance and the measurement system of length as discussed in Topic 1-1. Thus, any point
on the line can be represented by a real number, its distance from the origin O. The
assembly of all the points, each of which can be represented by a real number, is called
a one-dimensional space. Thus, the line under consideration is a one-dimensional space.
However, a one-dimensional space is more general than a straight line. A
curved line, open or closed, is also a one-dimensional space since each point on it can
also be represented by a real number, the distance from the origin that can be picked
artificially.
 A point on a flat surface can be determined by two real numbers. The easiest way to see
it is to draw two perpendicular lines and call one the x-axis and the other the y-axis.
Then each point on the surface has a distance to the x-axis and a distance to the
y-axis as shown in Fig. 2. In the figure the distance from point P to the y-axis
is Px, and the distance to the x-axis is Py. Thus the
point P can be represented by a pair of real numbers, (Px, Py).
On the other hand if we specify two distances, one from the x-axis and the
other from the y-axis, then a point on the surface can be uniquely determined. Thus any
point on the flat surface can be represented by two real numbers. The assembly of points
that can be represented by two real numbers is called a two-dimensional space. Of course,
a two-dimensional space does not need to be a flat surface. It can be any curved
surfaces; for example the surface of a sphere is a two-dimensional space.
A point on a flat surface can be determined by two real numbers. The easiest way to see
it is to draw two perpendicular lines and call one the x-axis and the other the y-axis.
Then each point on the surface has a distance to the x-axis and a distance to the
y-axis as shown in Fig. 2. In the figure the distance from point P to the y-axis
is Px, and the distance to the x-axis is Py. Thus the
point P can be represented by a pair of real numbers, (Px, Py).
On the other hand if we specify two distances, one from the x-axis and the
other from the y-axis, then a point on the surface can be uniquely determined. Thus any
point on the flat surface can be represented by two real numbers. The assembly of points
that can be represented by two real numbers is called a two-dimensional space. Of course,
a two-dimensional space does not need to be a flat surface. It can be any curved
surfaces; for example the surface of a sphere is a two-dimensional space.
 The space we live in is a three-dimensional space, each point on which can be
uniquely determined by a set of three real numbers. In Fig. 3 we show such an example.
Three mutually perpendicular lines are drawn, and are called x-, y- and z-
axes respectively. A point P is projected down to the x-y plane and its image
is denoted as point P'. The distance between P and P' is Pz. The
distance of P' to the x-axis is Py and the distance of P' to y-axis
is Px. Thus the point P can be represented as
(Px, Py, Pz). On the other hand the assembly
of the set of three continuous real numbers forms a three dimensional space.
It is difficult to explain anything
beyond the three-dimensional space in which we live except by going into the pure
mathematical definition of multi-dimensional spaces. One thing we can say is that our
three-dimensional space contains numerous two-dimensional and one-dimensional spaces.
The space we live in is a three-dimensional space, each point on which can be
uniquely determined by a set of three real numbers. In Fig. 3 we show such an example.
Three mutually perpendicular lines are drawn, and are called x-, y- and z-
axes respectively. A point P is projected down to the x-y plane and its image
is denoted as point P'. The distance between P and P' is Pz. The
distance of P' to the x-axis is Py and the distance of P' to y-axis
is Px. Thus the point P can be represented as
(Px, Py, Pz). On the other hand the assembly
of the set of three continuous real numbers forms a three dimensional space.
It is difficult to explain anything
beyond the three-dimensional space in which we live except by going into the pure
mathematical definition of multi-dimensional spaces. One thing we can say is that our
three-dimensional space contains numerous two-dimensional and one-dimensional spaces.
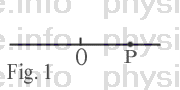 Let us consider a line, take a point on the line, and call it the origin, denoted as
O as in Fig. 1. We can determine a distance to any point P from the origin O, using the concept of
distance and the measurement system of length as discussed in Topic 1-1. Thus, any point
on the line can be represented by a real number, its distance from the origin O. The
assembly of all the points, each of which can be represented by a real number, is called
a one-dimensional space. Thus, the line under consideration is a one-dimensional space.
However, a one-dimensional space is more general than a straight line. A
curved line, open or closed, is also a one-dimensional space since each point on it can
also be represented by a real number, the distance from the origin that can be picked
artificially.
Let us consider a line, take a point on the line, and call it the origin, denoted as
O as in Fig. 1. We can determine a distance to any point P from the origin O, using the concept of
distance and the measurement system of length as discussed in Topic 1-1. Thus, any point
on the line can be represented by a real number, its distance from the origin O. The
assembly of all the points, each of which can be represented by a real number, is called
a one-dimensional space. Thus, the line under consideration is a one-dimensional space.
However, a one-dimensional space is more general than a straight line. A
curved line, open or closed, is also a one-dimensional space since each point on it can
also be represented by a real number, the distance from the origin that can be picked
artificially. A point on a flat surface can be determined by two real numbers. The easiest way to see
it is to draw two perpendicular lines and call one the x-axis and the other the y-axis.
Then each point on the surface has a distance to the x-axis and a distance to the
y-axis as shown in Fig. 2. In the figure the distance from point P to the y-axis
is Px, and the distance to the x-axis is Py. Thus the
point P can be represented by a pair of real numbers, (Px, Py).
On the other hand if we specify two distances, one from the x-axis and the
other from the y-axis, then a point on the surface can be uniquely determined. Thus any
point on the flat surface can be represented by two real numbers. The assembly of points
that can be represented by two real numbers is called a two-dimensional space. Of course,
a two-dimensional space does not need to be a flat surface. It can be any curved
surfaces; for example the surface of a sphere is a two-dimensional space.
A point on a flat surface can be determined by two real numbers. The easiest way to see
it is to draw two perpendicular lines and call one the x-axis and the other the y-axis.
Then each point on the surface has a distance to the x-axis and a distance to the
y-axis as shown in Fig. 2. In the figure the distance from point P to the y-axis
is Px, and the distance to the x-axis is Py. Thus the
point P can be represented by a pair of real numbers, (Px, Py).
On the other hand if we specify two distances, one from the x-axis and the
other from the y-axis, then a point on the surface can be uniquely determined. Thus any
point on the flat surface can be represented by two real numbers. The assembly of points
that can be represented by two real numbers is called a two-dimensional space. Of course,
a two-dimensional space does not need to be a flat surface. It can be any curved
surfaces; for example the surface of a sphere is a two-dimensional space. The space we live in is a three-dimensional space, each point on which can be
uniquely determined by a set of three real numbers. In Fig. 3 we show such an example.
Three mutually perpendicular lines are drawn, and are called x-, y- and z-
axes respectively. A point P is projected down to the x-y plane and its image
is denoted as point P'. The distance between P and P' is Pz. The
distance of P' to the x-axis is Py and the distance of P' to y-axis
is Px. Thus the point P can be represented as
(Px, Py, Pz). On the other hand the assembly
of the set of three continuous real numbers forms a three dimensional space.
It is difficult to explain anything
beyond the three-dimensional space in which we live except by going into the pure
mathematical definition of multi-dimensional spaces. One thing we can say is that our
three-dimensional space contains numerous two-dimensional and one-dimensional spaces.
The space we live in is a three-dimensional space, each point on which can be
uniquely determined by a set of three real numbers. In Fig. 3 we show such an example.
Three mutually perpendicular lines are drawn, and are called x-, y- and z-
axes respectively. A point P is projected down to the x-y plane and its image
is denoted as point P'. The distance between P and P' is Pz. The
distance of P' to the x-axis is Py and the distance of P' to y-axis
is Px. Thus the point P can be represented as
(Px, Py, Pz). On the other hand the assembly
of the set of three continuous real numbers forms a three dimensional space.
It is difficult to explain anything
beyond the three-dimensional space in which we live except by going into the pure
mathematical definition of multi-dimensional spaces. One thing we can say is that our
three-dimensional space contains numerous two-dimensional and one-dimensional spaces.